Ông già Erastosthenes ngầu cỡ nào (kỳ 2)
Bởi vậy nên mới nói ổng ngầu. Ngầu ở chỗ tính ra con số chính xác đã đành, mà ngay cả khi dám đặt bút xuống tính cho ra chu vi Trái Đất trong thời buổi mà phương tiện đo đạc không chính xác, đơn vị đo đạc cũng chưa hoàn thiện, là nhất rồi.
Kỳ trước tôi nói về sieve of Eratosthenes, sàng Eratosthenes, một phương pháp sàng lọc ra số nguyên tố mà tới ngày nay, 2200 năm sau, vẫn còn có ảnh hưởng trong những ngành hi-tech. đủ thấy Eratosthenes ngầu cỡ nào rồi. Kỳ này tôi nói về một con Toán ổng làm còn ngầu hơn.
Mở ngoặc nói về phát âm tên ông Eratosthenes. Ở Việt Nam nhiều người phát âm theo tiếng Pháp Ératosthène Ê-ra-tô-xten còn ở Mỹ thì phát âm luôn chữ s cuối, nên đọc là E-rơ-TOS-the-niz, với th phát âm như trong think. Rất nhiều tên Hy Lạp vào tới Mỹ là chữ s cuối phát âm ra tiếng luôn, thí dụ như Archilles phát âm là ARC-ki-liz.
Bài toán của Eratosthenes tôi muốn kể ở đây là bài toán đo kích thước của Trái Đất. Eratosthenes đo được chu vi vòng quanh (viên chu) Trái Đất chính xác gần sát với con số thật. Mở thêm một ngoặc nữa là thời Hy Lạp cổ người ta đã biết Trái Đất hình cầu rồi nha, không như một số người thời nay cứ cãi là Trái Đất phẳng lỳ.
Ở phía bắc Syene (nay là Aswan, Ai Cập) có một cái giếng sâu, được nổi tiếng vì hàng năm cứ đúng giữa trưa ngày Hạ chí, mặt trời chiếu thẳng xuống đáy giếng. Nhưng ở Alexandria, nơi Eratosthenes làm Trưởng Quản thủ Thư viện Alexandria huyền thoại, thì cũng ngày đó giờ đó mặt trời chiếu không thẳng mà có bóng. Ông mới nghĩ ra cách đo khoảng cách vòng quanh Trái Đất.
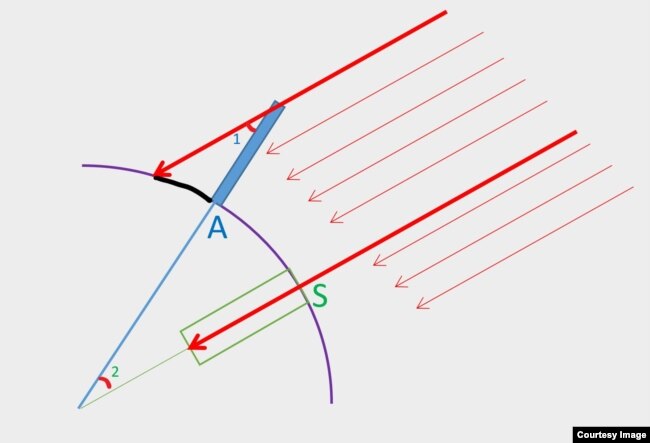
Vì mặt trời ở cực kỳ xa Trái Đất, nên có thể xem như tia nắng mặt trời xuống tới Trái Đất là song song. Tia nắng đã song song thì cái bóng ở Alexandria là do độ cong của mặt đất. Từ đó tính ra chu vi. Ông chứng minh bằng sơ đồ giống như vầy.
Ở điểm S, Syene, là cái giếng. Ở điểm A, Alexandria, là một cái tháp. Do tia nắng song song, nên góc số 1 ở Alexandria với góc số 2 ở trung tâm Trái Đất là bằng nhau, vì là góc so le (tiếng Anh gọi là alternate interior angles, AIA).
Eratosthenes đo ra góc số 1 là 1/50 hình tròn. (Thời đó chưa có số đo vòng tròn 360 độ; cái đó phải chờ tới văn minh Babylon mới có.) Vậy góc số 2 ở trung tâm Trái Đất cũng là 1/50 hình tròn. Vậy chu vi vòng quanh Trái Đất phải là 50 lần khoảng cách từ Syene tới Alexandria, cứ thế nhân lên thì biết.
Và Eratosthenes cứ thế nhân lên, tính ra chu vi vòng quanh Trái Đất là 250,000 stadia.
Stadia là số nhiều của stadion. Một stadion là khoảng cách chung quanh một sân vận động. Mà tất nhiên là mỗi sân vận động là mỗi khác, nên ngày nay có nhiều ý kiến khác nhau và chiều dài của một stadion thời Hy Lạp cổ, cách xa từ 157 m tới 185 m. Sách Hy Lạp cổ có ghi lại là 1 stadion = 600 podes (bộ Hy Lạp, số ít là pous), nhưng 1 pous bằng bao nhiêu thì cũng tranh cãi luôn. Nếu tính theo 157m thì đáp số của Eratosthenes có sai số –2%, và nếu tính theo 185 m thì sai số +15%. Sai số cỡ đó là quá hay rồi. Ngay cả ngày nay đem dụng cụ phòng thí nghiệm cho học sinh làm thì sai số cũng cỡ đó hoặc còn hơn thế nữa.
Nhưng thực ra không cần giải quyết một stadion là bao nhiêu. Chỉ cần biết Eratosthenes tính 50 lần khoảng cách từ Syene tới Alexandria ra chu vi vòng quanh Trái Đất. Vậy mình cũng nhân 50 lần khoảng cách từ cái giếng ở Syene tới Alexandria. Khoảng cách này xấp xỉ 800 km theo đường chim bay. Nhân với 50 thì bằng 40,000 km. Chu vi Trái Đất vòng quanh đường xích đạo là 40,075 km, sai số –0.19%.
Tóm lại là vầy. Eratosthenes sống vào thời tương đương Thục Phán An Dương Vương, tức là trước cả thời Bắc thuộc. Lúc đó chưa có Việt Nam, chưa có An Nam, chưa có cả Giao Chỉ. Vậy mà ông tính được đường chu vi vòng quanh Trái Đất, với sai số có thể chỉ có 0.19% và tệ lắm là 15%.
Bởi vậy nên mới nói ổng ngầu. Ngầu ở chỗ tính ra con số chính xác đã đành, mà ngay cả khi dám đặt bút xuống tính cho ra chu vi Trái Đất trong thời buổi mà phương tiện đo đạc không chính xác, đơn vị đo đạc cũng chưa hoàn thiện, là nhất rồi.